
Cómo calcular la Deflexión de una Viga: Porque el diseño de las vigas se rige con frecuencia por la rigidez más que por la resistencia. Por ejemplo, las normas de construcción especifican límites en las deflexiones y las tensiones.
La deflexión excesiva de una viga no solo es visualmente molesta, sino que también puede causar daños a otras partes del edificio. Por esta razón, las normas de construcción limitan la deflexión máxima de una viga a aproximadamente 1/360 de sus vanos.
Se dispone de varios métodos analíticos para determinar las deflexiones de las vigas. Su base común es la ecuación diferencial que relaciona la deflexión con el momento flector. La solución de esta ecuación es complicada porque el momento flector suele ser una función discontinua, por lo que las ecuaciones deben integrarse a trozos.
¿Cómo calcular la Deflexión de una Viga? Guía práctica y Ejemplos
Deflexión, en términos de ingeniería estructural, significa el movimiento de una viga o nodo desde su posición original. Ocurre debido a las fuerzas y cargas que se aplican al cuerpo. Deflexión, también conocida como desplazamiento, que puede ocurrir por cargas aplicadas externamente o por el peso de la propia estructura de la carrocería. Puede ocurrir en vigas, cerchas, marcos y básicamente cualquier otra estructura de carrocería. En este artículo, analizaremos la fórmula de deflexión de la viga con ejemplos. ¡Aprendámoslo!
Por si es de tu interés saber un poco más sobre este tema de Deflexión en Vigas, Visita nuestras entradas que aquí abajo adjunto!

¿Cómo se mide la deflexión en estructuras?

Qué es Deflexion

Cálculo de Deflexión en la Viga Benkelman

Deflexión en Vigas Método de Superposición

Deflexión en Vigas Hiperestáticas

Deflexión en Vigas Ejercicios Resueltos
Fórmula de deflexión de Viga
¿Qué es la desviación de la Viga?
La deflexión es el grado en que un elemento estructural particular puede desplazarse con la ayuda de una cantidad considerable de carga. También puede denominarse ángulo o distancia. La distancia de deflexión de un miembro bajo una carga está directamente relacionada con la pendiente de la viga deflectada del cuerpo bajo esa carga. Se puede calcular integrando la función que se utiliza para describir la pendiente del miembro bajo esa carga.
La viga es una pieza larga de un cuerpo que es capaz de soportar la carga resistiendo la flexión. La deflexión del haz hacia una dirección particular cuando se le aplica una fuerza se conoce como deflexión de la viga.
La viga se puede doblar o alejar de su posición original. Esta distancia en cada punto a lo largo del miembro es la representación de la deflexión. Existen principalmente cuatro variables que pueden determinar la magnitud de las deflexiones del haz. Éstas incluyen:
- ¿Cuánta carga hay sobre la estructura?
- La longitud del miembro sin soporte.
- El material, específicamente el Módulo de Young
- El tamaño de la sección transversal, específicamente el momento de inercia(I)
Existe una variedad de ecuaciones de deflexión de vigas que se pueden utilizar para calcular un valor básico de deflexión en diferentes tipos de vigas. Generalmente, calculamos la deflexión tomando la integral doble de la ecuación del momento flector M(x) dividida por el producto de E e I (es decir, módulo de Young y momento de inercia).
La unidad de deflexión, o desplazamiento, será una unidad de longitud y normalmente la medimos en un milímetro. Este número define la distancia a la que el haz puede desviarse de su posición original.
La fórmula para la deflexión del haz
Las vigas en voladizo son tipos especiales de vigas que están limitadas por un solo soporte determinado. Este tipo de objetos, naturalmente, se desviarían más debido a que tienen soporte en un solo extremo. Para calcular la deflexión de la viga en voladizo podemos usar la siguiente ecuación:
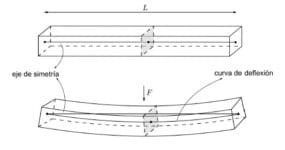
La curva que describe la deformación que experimenta la viga al aplicar una carga sobre ella se conoce como curva de deflexión o curva elástica, u(x).
1. Viga simplemente apoyada con carga uniformemente distribuida:
y = (5/384) * (w * L^4) / (E * I)
Donde:
- y: Deflexión en el centro de la viga (metros)
- w: Carga uniformemente distribuida (N/m)
- L: Longitud de la viga (metros)
- E: Módulo de Young del material de la viga (N/m^2)
- I: Momento de inercia de la sección transversal de la viga (m^4)
2. Viga en voladizo con carga puntual en el extremo libre:
y = (P * L^3) / (3 * E * I)
Donde:
- y: Deflexión en el extremo libre de la viga (metros)
- P: Carga puntual (N)
- L: Longitud de la viga (metros)
- E: Módulo de Young del material de la viga (N/m^2)
- I: Momento de inercia de la sección transversal de la viga (m^4)
